最も簡単な流体シミュレーション・ソフトウェア

咳による飛沫の広がりのシミュレーション
1.はじめに
様々なウイルス感染メカニズムの一つと考えられている咳による飛沫の広がり方のシミュレーション例です。本シミュレーションでは、咳による口元からのガスの濃度(質量分率)の広がりを観察します。本入力ファイルに様々な障害物を追加して、飛沫の広がり方の変化を予測することもできます。
題材は、GRABCADにて公開されている人物モデルです。リンク切れ等でGRABCADからダウンロードできない場合は、こちらからでもSTLファイルをダウンロードすることも可能です。
本シミュレーション前に、『CAD(STL)モデルとその最適化』を参考に元STLファイルのスケール(人物の身長等)を適切に設定します。最適化後のSTLは、以下からダウンロード可能な入力ファイル一式に含まれます。
ここで紹介するシミュレーション実行に必要な全ての入力ファイルは、以下からダウンロードできます。zipファイルをダウンロードする場合、FSPフォルダまたはその階層以下のフォルダに展開してください。※シミュレーション実施前に、param_0.txtとparam_100.txtは適宜ファイル名をparam.txtに変更してください。
入力ファイル
- param_0.txt(0~100ステップまで;初期フェーズ用;param.txtに要変更)
(2022R3.1以前のバージョンの場合、こちらを使います) - param_100.txt(100ステップ以降;中期フェーズ用;param.txtに要変更)
(2022R3.1以前のバージョンの場合、こちらを使います) - bcXY0.bmp
- bcZX0.bmp
- bc.stl
また、本シミュレーションは、一般的なIntel COREi7搭載のノートパソコン上で、最大並列数(parallel)を用いて、1000ステップ20分程度の計算速度です。
2.計算対象・境界条件
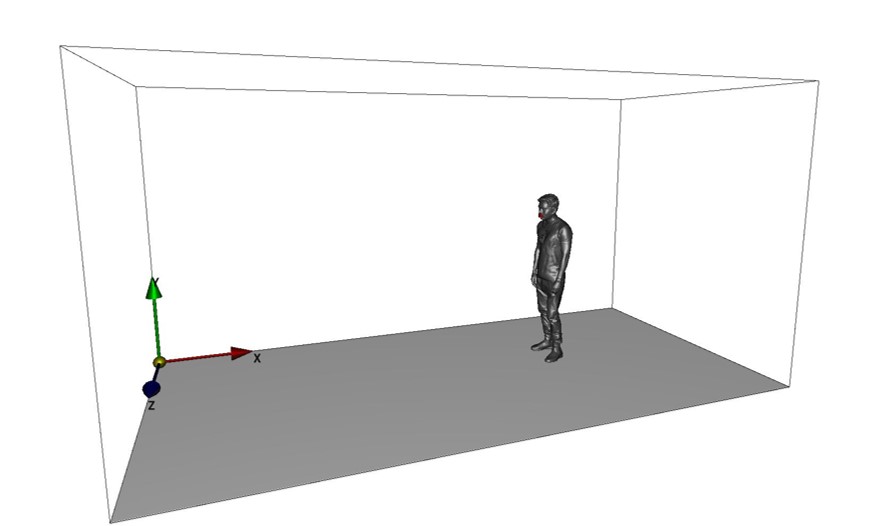
シミュレーション系は、地面に身長約190㎝である人物モデルが起立しており、口元の位置に赤色境界を設けています。人物モデルはSTLファイルで、赤色境界は、ビットマップ画像で指定しており、ちょうど人物の口元に赤色境界が一致するように境界条件設定画像を調整します(上記からダウンロードできる入力ファイルは既に調整済みです)。赤色境界の位置や形状は、もう少し詳細に指定してもよいでしょう。

3.計算パラメータの設定
以下は、本シミュレーションにおいて特に大事なパラメータについての説明です。一般的な計算パラメータの説明は、こちらをご覧ください。
計算パラメータは、初期フェーズ(例では0~100ステップ)及びそれ以降の中期フェーズ(例では100ステップ以降)によって異なる2セットを用います。違いは以下のパラメータです。
初期フェーズ用
初期フェーズでは、赤色境界に初期速度として、左向き55m/s(約200km/h)の初期流速を与えます。咳は無限小の時間に行われるプロセスではなく、ある一定の時間をかけて発生する現象ですので、本シミュレーションでは、100ステップ分程度の時間、赤色境界から口元からのガスが流出するという設定とします。
また、咳により口元から流出するガスの質量分率は、赤境界では、100%ですので、この流入ガスの質量分率を1とします。ここで、咳による流体速度は、不確定性が大きく、多くの場合、200km/h~400km/hと考えられているようです。
- cfl = 0.25
- uinR = -55 m/s
- vinR = 0.0 m/s
- winR = 0.0 m/s
- massfrR = 1.0 m/s
中期フェーズ
初期フェーズ後、つまり咳をした後は、口元付近に設けた赤色境界は流体場に作用してはなりませんので、赤色で規定される流体速度(uinR, vinR, winR)及び質量分率(massfrR)はいずれも「-」(ハイフン)とします。これで、実質的に赤色境界は無効となります。パラメータを変更せずに、境界条件設定用のビットマップ画像を編集し、赤色境界を消去する、という方法でも構いません。
中期フェーズでCFLを小さくする(時間間隔を小さくする)理由ですが、徐々にシミュレーション領域内の最大流速が小さくなり、時間間隔の制約における拡散の影響が強く出てくるためです。
- cfl = 0.10
- uinR = -
- vinR = -
- winR = -
- massfrR = -
4.シミュレーション結果
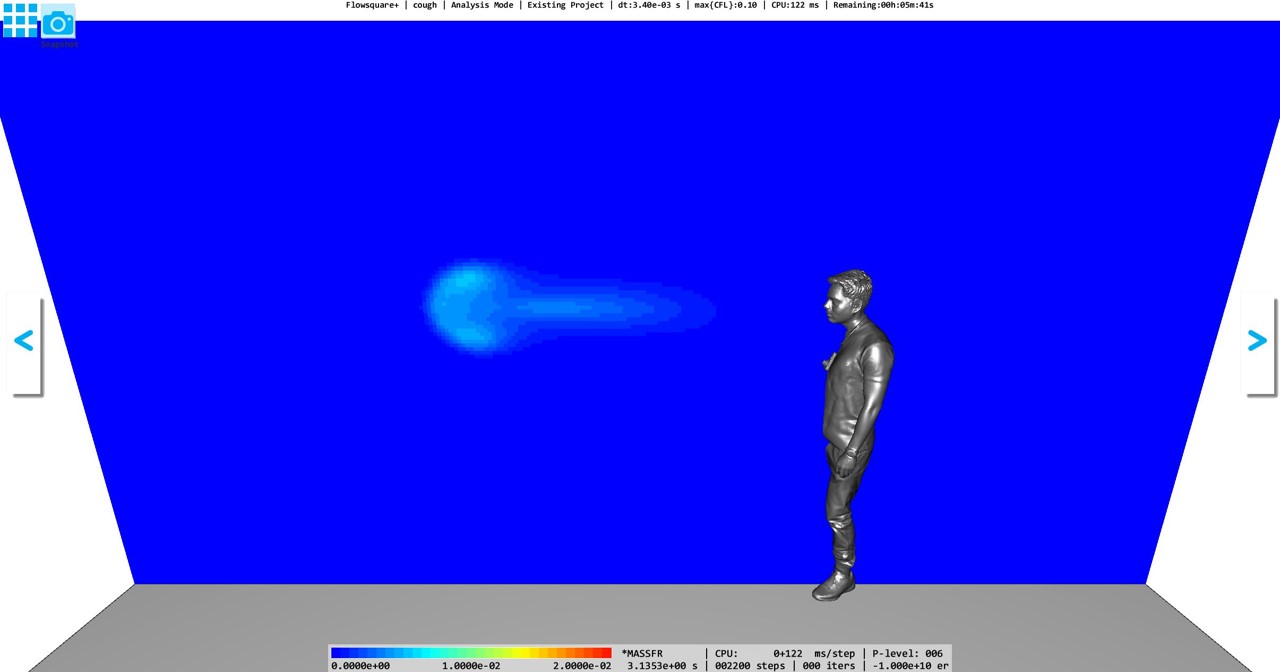
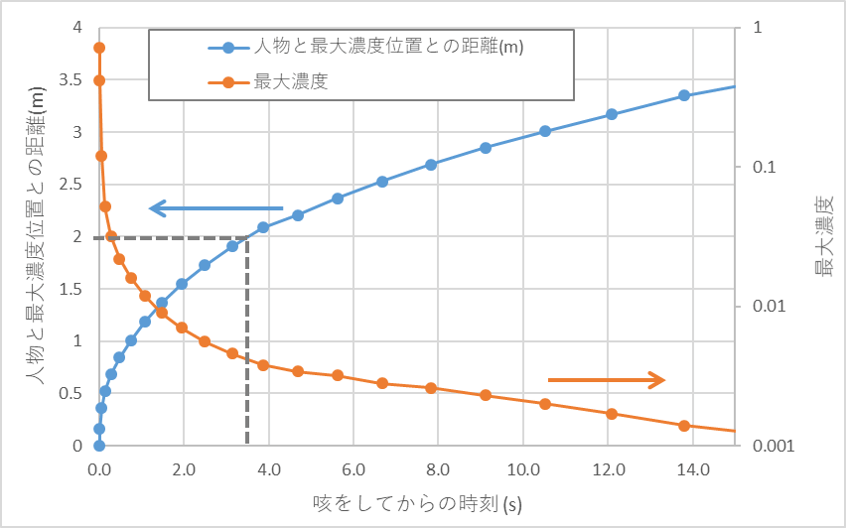
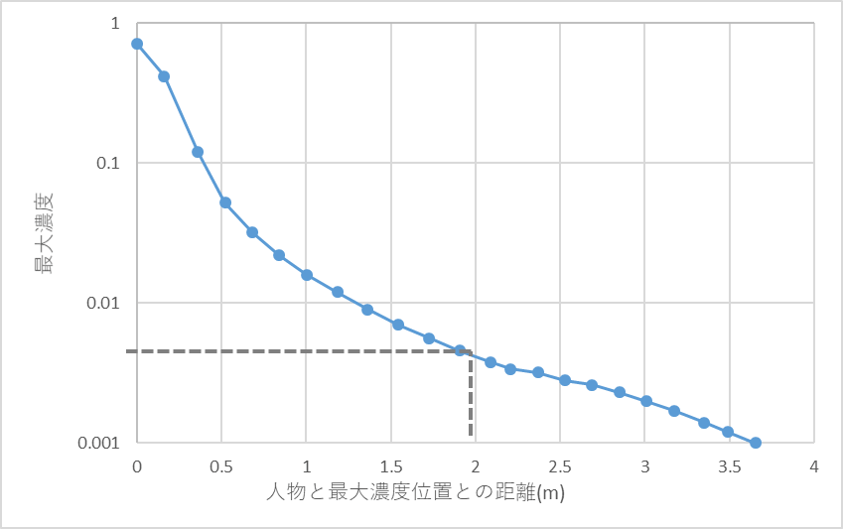
以下は、瞬時の飛沫の質量分率(濃度)の結果です。咳をした後、およそ3秒程度で飛沫が高濃度である領域は人物から水平方向に約2mまで移流し、濃度はおよそ1%(1.0E-02)以下まで低下します。下の動画で示す時間発展から観察されるように、この時刻以降は飛沫の移流の時間変化は緩やかになり、濃度の時間低下も緩やかになることが観察されます。
 EN
EN