最も簡単な流体シミュレーション・ソフトウェア
シミュレーションを向上させるヒント
1.はじめに
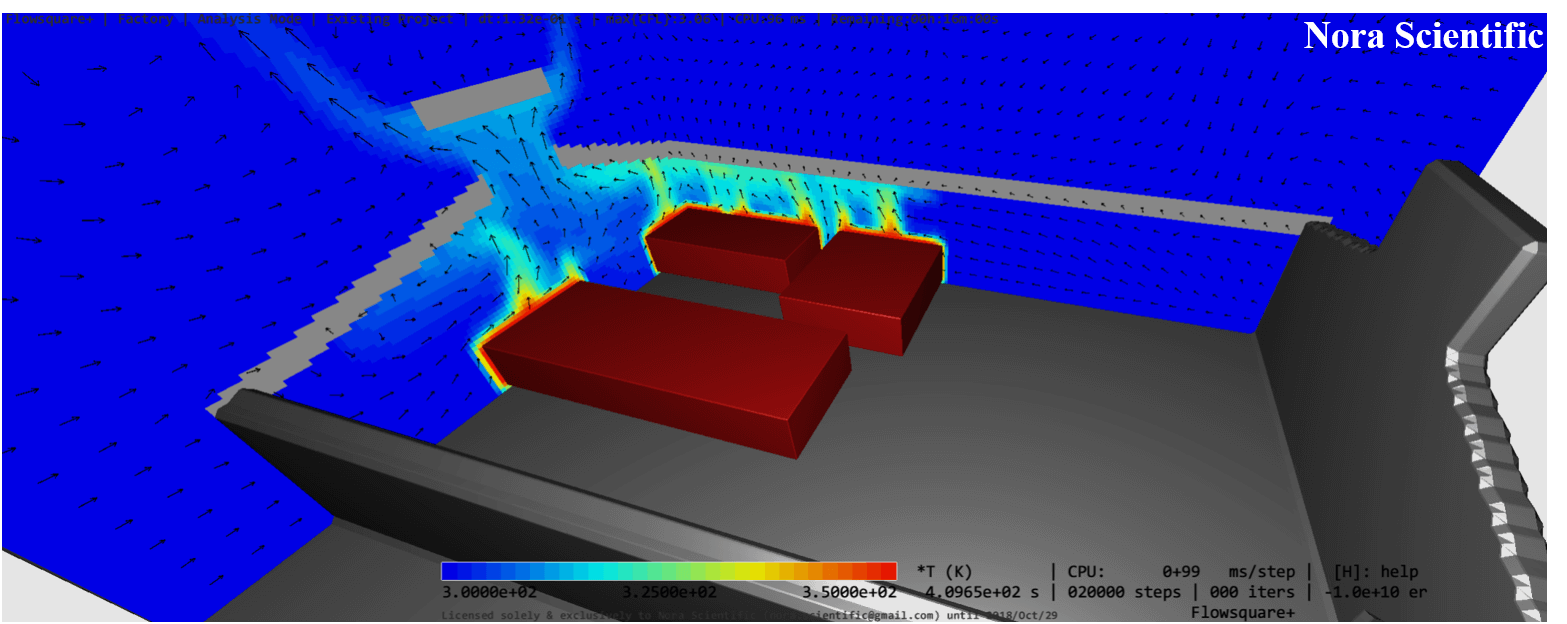
Flowsquare+と共に、公開されているシミュレーション例用入力ファイルを活用すると、どなたでも簡単に流体シミュレーションの実施が可能です。組み込み済みの様々な可視化手法により、シミュレーションされた流体速度場が直ちにグラフィカルに描画され、説得力のある流体解析結果を表示します。
本ページでは、単に流体シミュレーションを実施するだけではなく、正しい知見を得ることを目的として数値流体解析を実施される、比較的高度なユーザー向けに、数値熱流体解析精度を向上させるための、少し高度な知識をご紹介します。
より一般的な数値熱流体解析に関する説明は、『CFDの基本原理』をご覧ください。また、Flowsquare+で採用されている数値手法の詳細は、『ソルバーの詳細』に紹介します。
2.空間解像度の設定
空間解像度は、シミュレーション精度及びコスト(計算にかかる時間)に最も直接影響を与えるパラメータのひとつです。一般的に、全ての流体運動を正確に解析するには、高精度数値手法と共に、乱流の最小運動スケールであるコルモゴロフ長さ程度の格子点間隔 \(\Delta x\)、\(\Delta y\)、\(\Delta z\) を用いる必要があります。このような高精度数値計算は、直接数値計算(direct numerical simulations; DNS)と呼ばれます。DNSでは、膨大な格子点数 \(N_x\times N_y\times N_z\) や高精度数値手法のために計算負荷が非常に大きく、通常は、何万CPUを用いるスーパーコンピュータ上で数か月計算し続けてシミュレーションを実施します。
Flowsquare+では、計算コスト制約の観点及び流体の非定常現象を考量する必要性から、格子解像度以下の流体現象の影響を考慮する乱流モデル(SGSモデル)を採用しています。これにより、DNSと比べて格段に少ない格子点数 \(N_x\)、\(N_y\)、\(N_z\) におけるシミュレーションでも、ある程度正確な流れ場の予測が可能です(もちろんモデル精度に対する格子点数の影響を予め見積もるのが理想ですが)。
一方で、格子解像度以下の物理境界(壁など)の影響は、どの乱流モデルを用いても考慮することはできません(例:格子点間隔より小さく湾曲するような壁面形状は考慮されない)。したがって、対象となる物理境界(と可能であれば乱流モデル)を考慮して、格子点数を決定する必要があります。
とは言うものの、一般PC上での数値流体解析における使用格子点数は、計算資源(メモリ・計算時間)の制約で決定される場合が殆どです。したがって、形状モデルや計算領域の最適化を行ったうえで、お使いのPC及び許容計算時間内で最も多くの格子点数を用いるという判断基準も現実的には悪くはないでしょう。
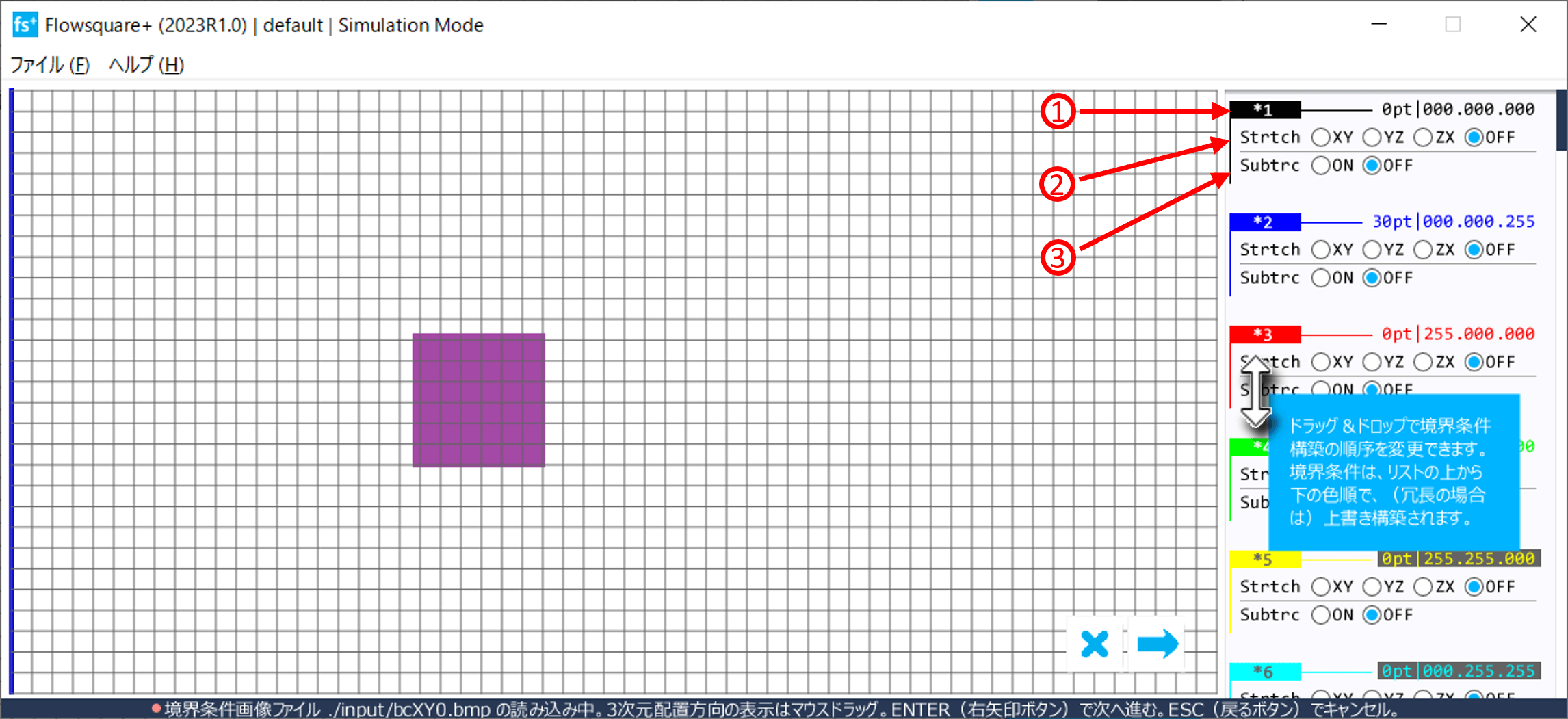
ちなみに、物理境界条件を解像するのに十分な格子を用いているか否かの判断を補助するために、Flowsquare+では境界条件設定用画像ファイル読み込み画面において、パラメータ設定画面で設定された格子を重ねて表示します。本画面において、壁面境界条件が設定された格子点によって再現できることを確認してください。重要な壁面形状が十分再現されない場合、格子点数を適宜調整します。
3.考慮する物理時間の判断
シミュレーション中の時間ステップ幅 \(\Delta t\) が一定の場合、シミュレーションにおける現在の物理時間は、現在の時間ステップ数\(\times\Delta t\) と計算されます。もっとも、Flowsquare+では各時間ステップにおいて最適な \(\Delta t\) を動的に調節していますので、現在の物理時刻は、シミュレーション画面において確認できます。または、各プロジェクト./dump/フォルダ内の出力ファイルにおいても確認可能です。
Flowsquare+では、シミュレーション開始方法として初期流体場(uinW、vinW、winW、rhoW、tempW、massfrW)などから構築されるインパルス・スタートを採用しています。多くの流体シミュレーションでは、シミュレーション開始から十分時間が経つまでは、シミュレーション結果は初期場の影響を大きく受けています。したがって、初期場からの遷移過程に着目することが目的でない多くの場合、初期場の影響が無視できる時刻までシミュレーションを実施する必要があります。
この『初期場の影響が無視できる時刻』は、以下のような方法で推定することができます。
- もっとも簡単な、必要シミュレーション時間の見積もりは、領域の大きさと主流速度の大きさを用いる方法です。単純に、領域の代表長さ \(L\) (m)と代表速度 \(U\) (m/s) を用いて、領域内の流体の時間スケール \(\tau\)は、\(\tau = L/U\) (s) と算出されます。この時間スケールの 5~10 倍程度以上の物理時間のシミュレーションを行うことで、シミュレーション結果に対する初期場の影響を十分小さくすることができます。
- もっとも確実な方法は、Flowsquare+のプローブ機能を用いる方法です。以下の図に示す、ある流体場に設置したプローブにて計測の流体速度の時間変化は、\(t=1.5\) 秒付近で準定常状態に完全に移行したと示されます。したがって、物理時間において \(t=1.5\) 秒以上のシミュレーション実施が望ましいと考えられます。同様の知見は、プローブを用いずとも、パラメータで指定する nfig ごとに出力される画像出力の時間変化を見ることでも得ることができるでしょう。
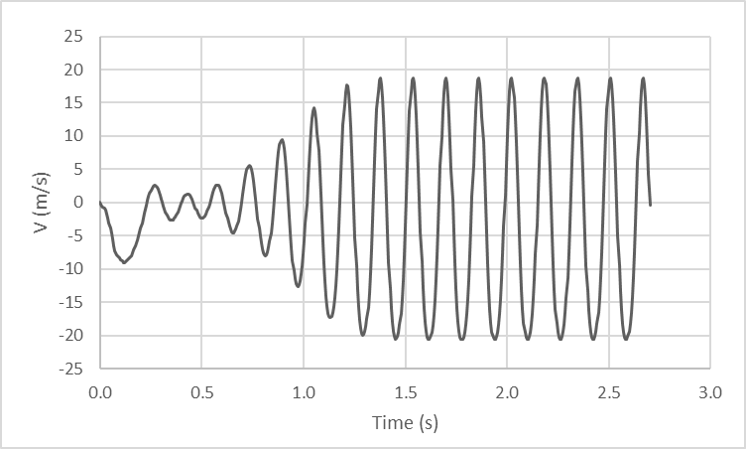
プローブにて計測された速度の時系列変化。
上記の物理時間に相当する時間ステップ数は、計算領域と格子点数、流体速度、CFL数等に依存する為、一概に何ステップ以上と判断することはできませんが、数千~数万ステップ以上のシミュレーションが必要であるケースが殆どです。
4.シミュレーション領域の選択
シミュレーション領域の境界(計算境界)上が、開放境界となっているシミュレーションを実施する場合、特に注意が必要です。詳しい理由は除きますが、対象となる領域内の物体と計算境界上の開放境界との間の距離が小さすぎると、シミュレーション領域内部の流れ場の予測に悪影響を及ぼします。ここで、どのような距離が小さすぎるのかの判断は容易ではありませんが、少なくとも物体の長さ以上の距離を流出境界との間に設けておくのが無難です(もちろん高速な流れの場合、物体長さの 10 倍以上の距離を設けることもあります)。
5.反復計算許容誤差の選択
パラメータで指定する peps や loopmaxは、それぞれ毎ステップ実施される反復収束計算における許容誤差と最大反復回数を決定します。より小さな peps やより大きな loopmax は、シミュレーション精度を向上させますが、計算速度は低下します。あまりにも大きな peps や小さな loopmax は、計算負荷は低減しますが、計算精度も低下し、最悪の場合、シミュレーションが発散し継続できなくなることもあります。通常は、既定値で問題ありませんが、状況に応じて、既定値を基準として調整すると良いでしょう。
 EN
EN