無料で使えて手軽な流体シミュレーション・ソフトウェア
EN
大型看板に働く流体力の計算
1．はじめに
ここでは、大型の広告看板などに働く流体力を流体シミュレーションから求めます。そして、考察を通じて、実務で用いられる抵抗係数に基づく流体力の推定方法（例：国交省による風荷重の算出基準）が、どの程度現実的な条件でも信頼性があるのかについて議論します。
シミュレーションを用いない場合の流体力の見積もり方法として、抵抗係数を用いる方法がよく知られています。抵抗係数\(C_D\)を用いると、流体力\(F_D~\rm{(N)}\)は、
\begin{equation} F_D=C_D \frac{\rho u^2}{2}A・・・式(1) \end{equation}で表され、ここで、\(\rho~\rm{(kg/m^3)}\)は流体密度（一定）、\(u~\rm{(m/s)}\)は流体速度、\(A~\rm{(m^2)}\)は物体の主流方向投影面積です（単位系はここではSI単位です）。
主流方向に垂直に設置された看板のような平板にかかる抵抗係数\(C_D\)は、平板のアスペクト比に依存します。平板の短辺長さを\(a\)及び長辺長さを\(b\)としたとき、
- \(a/b\sim1\) ⇒ \(C_D\approx1.1\)
- \(a/b\sim4\) ⇒ \(C_D\approx1.2\)
- \(a/b\sim10\) ⇒ \(C_D\approx1.3\)
- \(a/b\sim20\) ⇒ \(C_D\approx1.4\)
となることが知られています。ただし、これらの値は、\(C_D\)がおよそ一定であるレイノルズ数の範囲における代表値であることに注意します。また、平板は壁面や地面から十分離れた距離に設置してあり、物理境界の影響を受けない場合の計測値です。
本チュートリアルでは、広告看板をモデル化した境界条件をペイント画像を用いて構築し、構築した物体回りの流体シミュレーションを実施し、看板にかかる抵抗力を求めます。比較参考のために、抵抗係数の計測のように物理境界の影響が小さい条件下での、流れ方向に対して垂直に設置された平板周りのシミュレーションも実施します。また、抵抗係数\(C_D\)に基づいて推定した抵抗力と比較します。
ここで紹介するシミュレーション実行に必要な全ての入力ファイルは、以下からダウンロードできます。
（A）広告看板モデル
（B）平板モデル（流れ方向に対して垂直に保持され、他の物理境界の影響を受けない平板）
また、本シミュレーションは、一般的なIntel COREi7搭載のノートパソコン上で、最大並列数（parallel = 4）を用いて、1000ステップ10分程度の計算速度です。
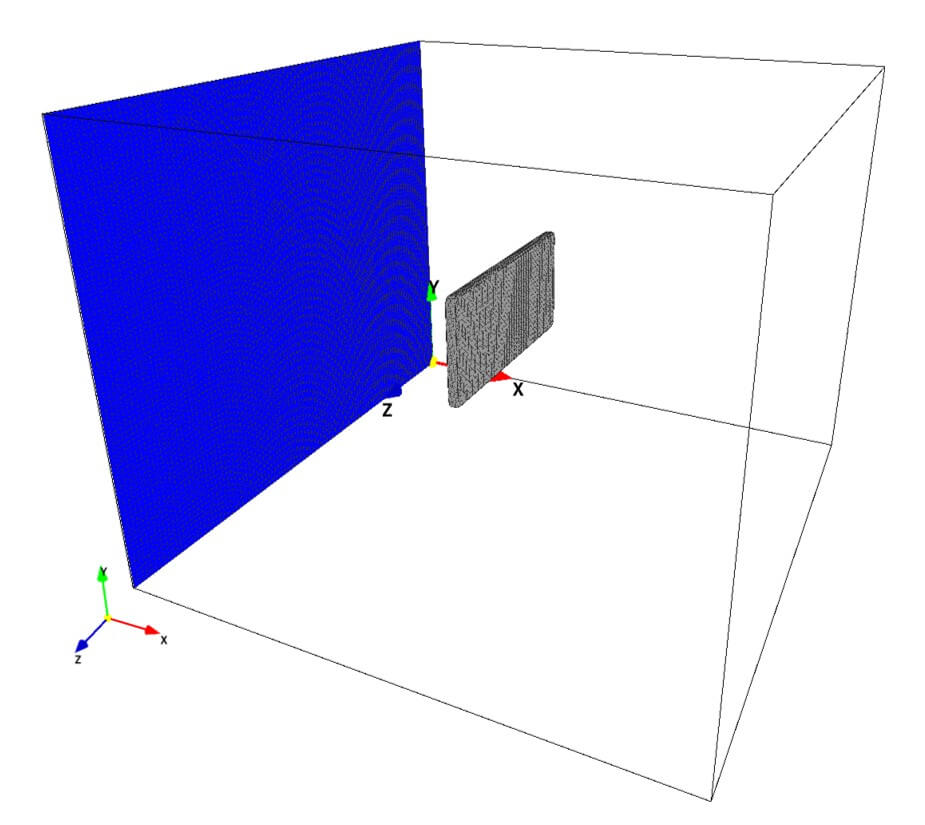
2．3次元モデル構築
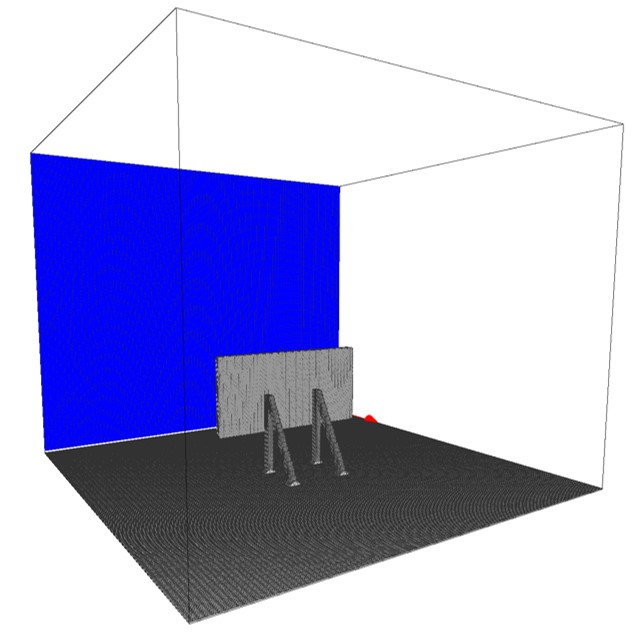
（A）広告看板モデル
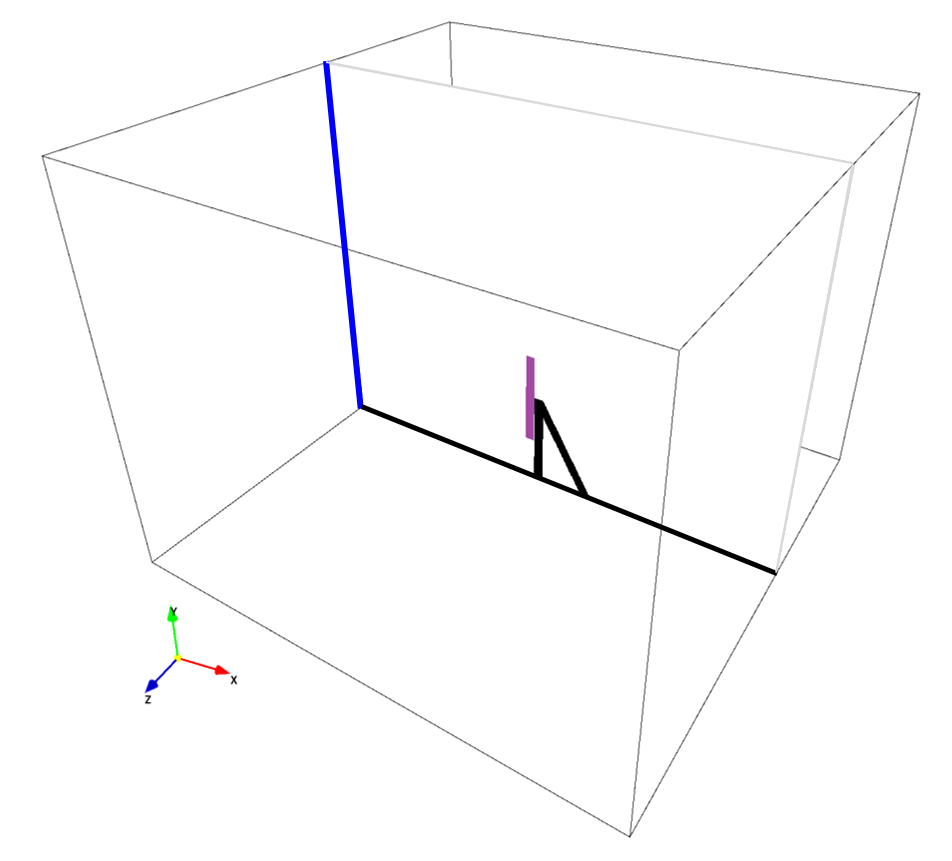
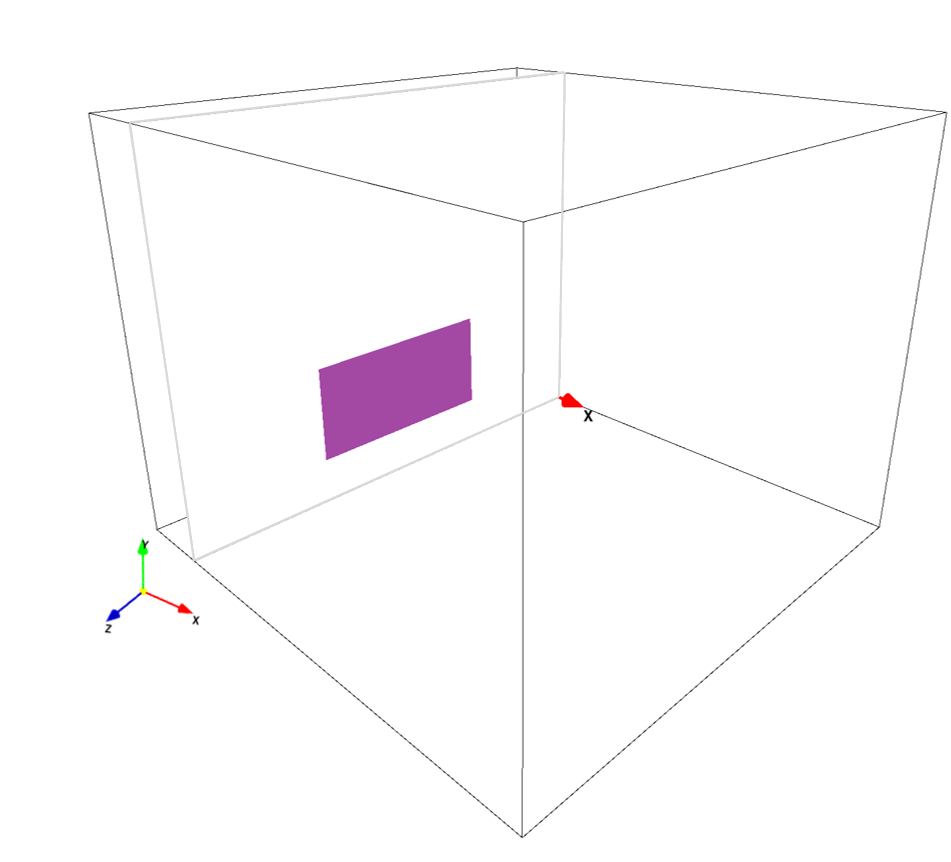
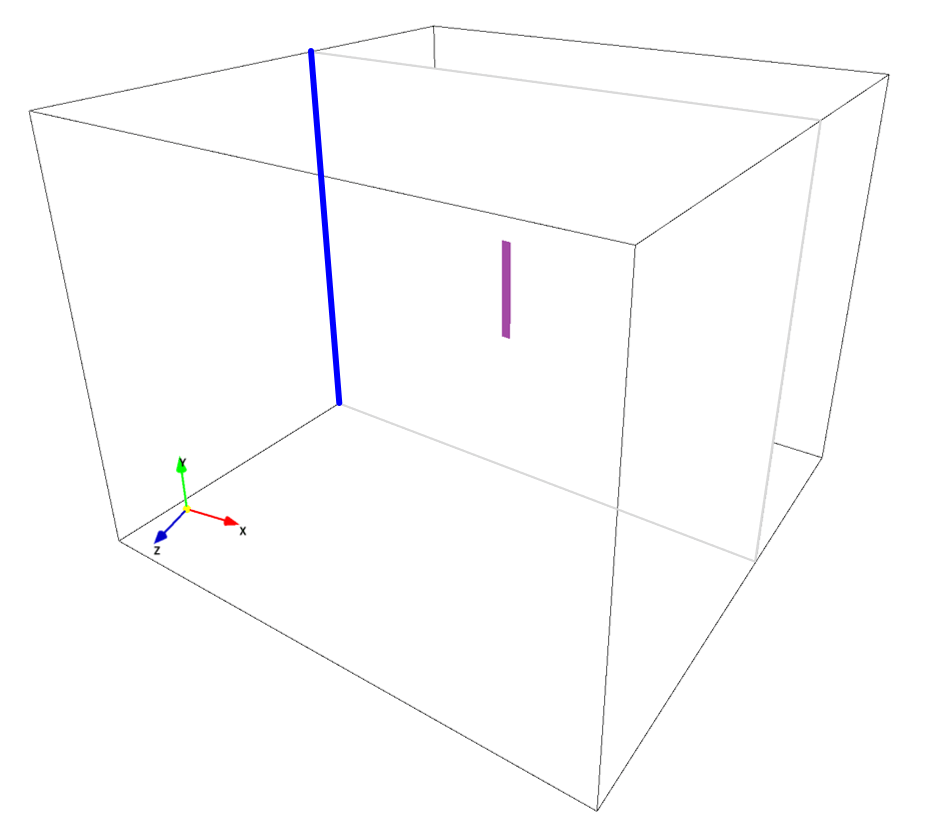
ペイント画像を用いた3次元モデル作成における基本的な構築ルールは、こちらのページをご覧ください。本シミュレーションにおいては、以下のような平面方向を有する3枚のペイント画像を利用して、看板モデルを構築します。以下の画像における色及びその色で構築されている境界は、
- 壁境界：看板本体、非プリセット・紫色
- 壁境界：看板支柱及び地面、プリセット・黒色
- 流入境界：プリセット・青色
の3項目を別々の色を用いて指定します。今回は、看板のみに働く流体力を計算できるように、看板本体を非プリセット色で指定し、その他の壁境界は黒（プリセット色）で指定しています。もちろん看板を黒で指定し、その他の物体を非プリセット色で指定しても問題ありません。
各画像のピクセル数に関して、厳密に計算領域サイズの縦横比に比例させる必要はありません。最終的な縦横サイズは、パラメータにて設定した物理サイズとなり、ソフトウェアで画像の補間処理を実施します。しかし、基本的には、ある程度サイズの縦横比を反映させるほうが、画像作成上便利です。
ここでは、入力画像全て物理サイズ1cmに対し2ピクセルで作成しています。画像ファイルにおいて、看板・平板サイズは、400ピクセル×200ピクセルであるため、その物理サイズは\(A=2\times1~\rm{(m^2)}\)です。
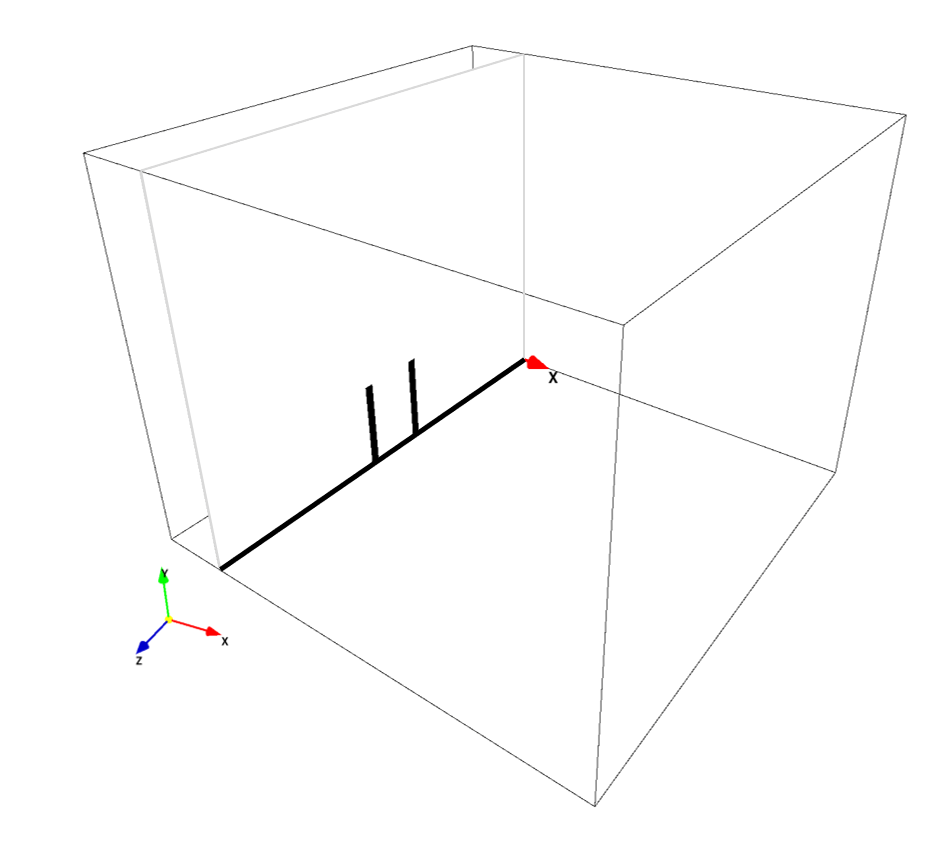
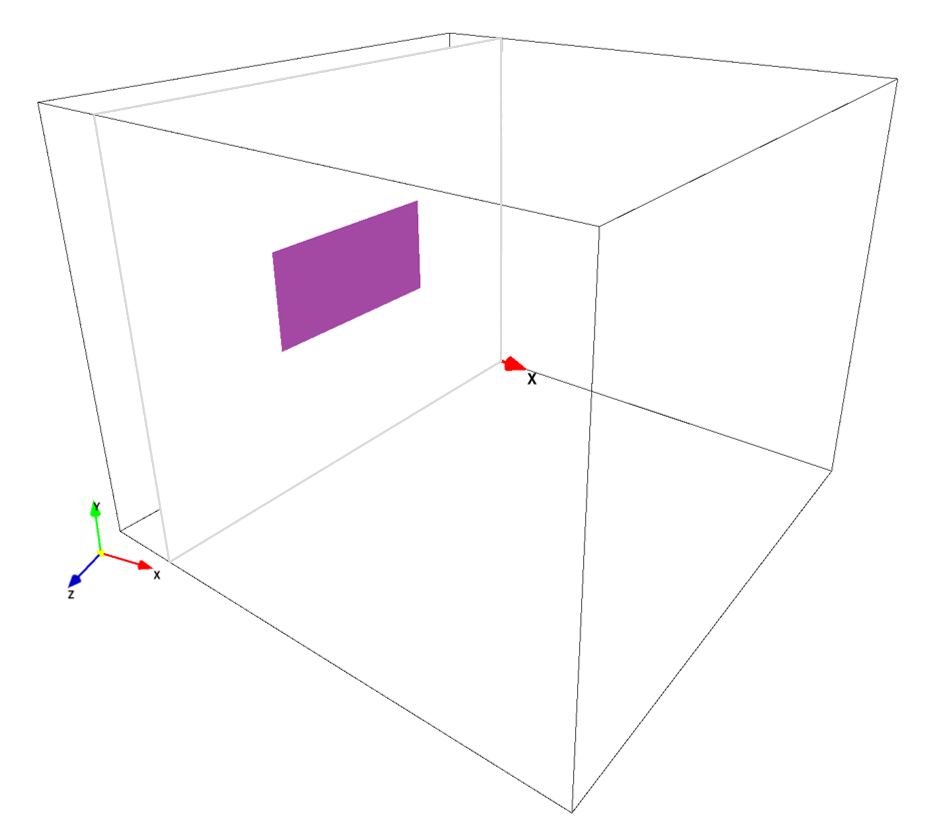
（B）平板モデル
こちらは、単に領域中央部、宙に浮いた平板ですので、2枚のペイント画像で構築可能です。平板サイズは、広告看板のサイズと同様です。
3．計算パラメータの設定
以下は、本シミュレーションにおける主なパラメータについての説明です。パラメータは（A）広告看板モデル及び（B）平板モデルで共通です。一般的な計算パラメータの説明は、こちらをご覧ください。- cmode
0の流体解析モードを選択 - lx
x方向領域サイズは5m。 - ly
y方向領域サイズは4m。 - lz
z方向領域サイズは5m。 - nx、ny、nz
(nx, ny, nz) = (400, 80, 100) - uinW
初期x方向流体速度は10m/sと指定。残りの領域内初期速度成分（vinW, winW）は0.0m/s（ゼロ）であり、これは既定値であるので、特に指定しなくてもよい。 - vinB
青色境界からの流入速度は10m/sと指定。他の速度成分（vinB, winB）は0.0m/s（ゼロ）であり、これは既定値であるので、特に指定しなくてもよい。
4．シミュレーションの実行、解析及び考察
いよいよシミュレーションを開始します。シミュレーションを十分長く実施し、初期条件場の影響が十分に小さくなったことを確認するために、後流領域にプローブを設置し、準定常状態に達したことを確認すると良いでしょう。
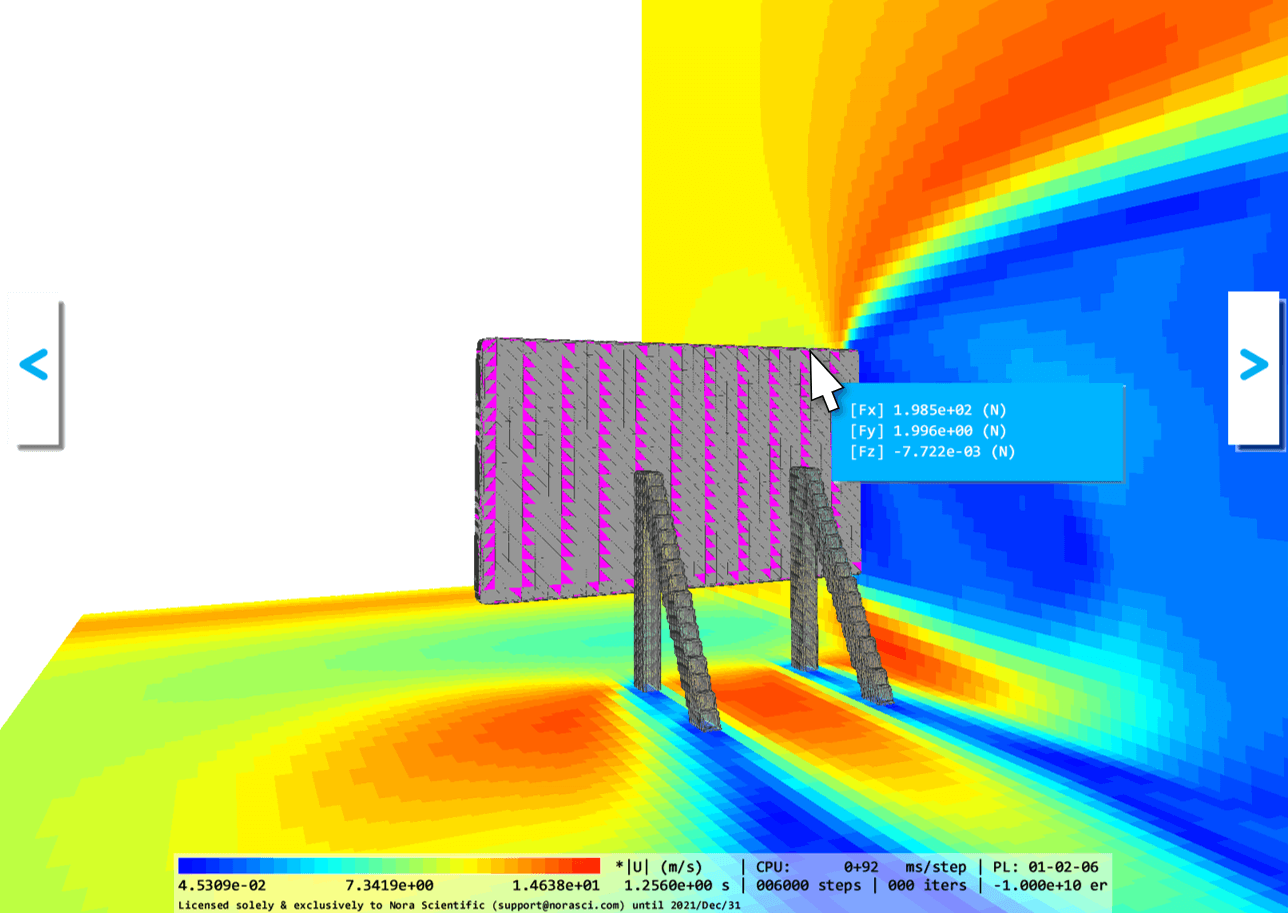
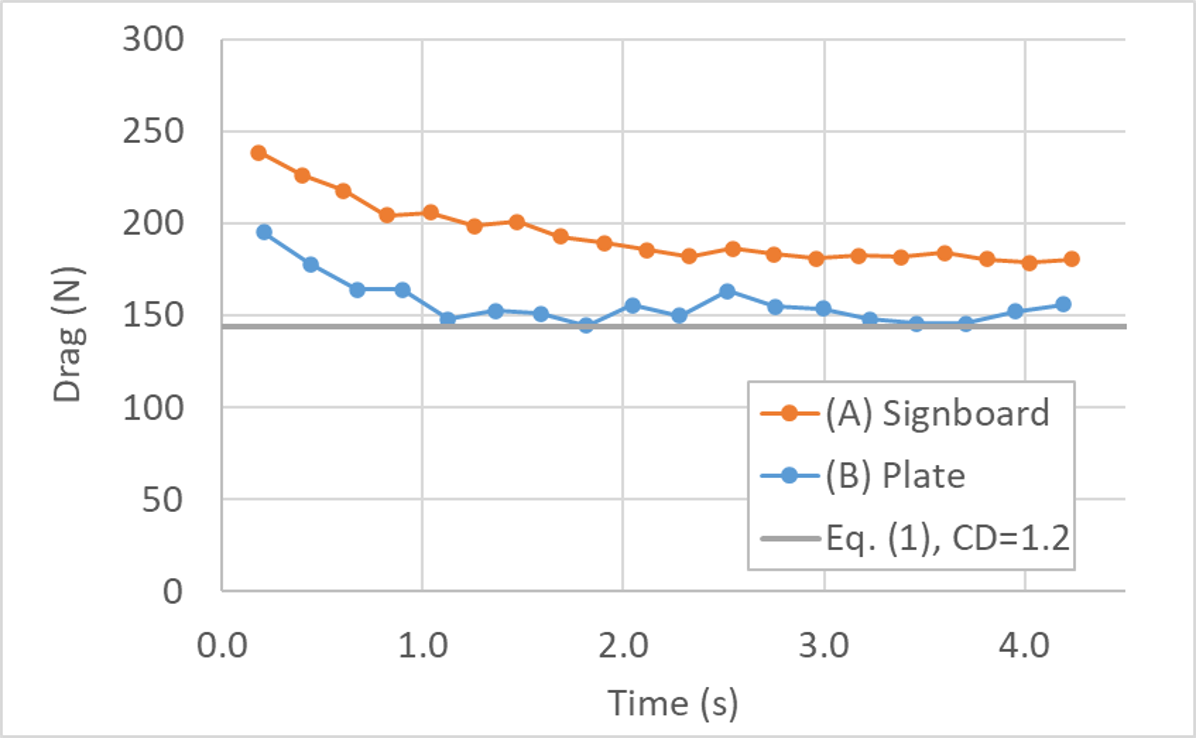
ツールメニュー内の
を用いると、シミュレーション中やシミュレーション後に看板や平板に働く流体抵抗を算出することができます。また、シミュレーション条件である\(\rho=1.2~\rm{(kg/m^3)}\)、\(u=10~\rm{(m/s)}\)、\(A=2~\rm{(m^2)}\)及び\(C_D=1.2\)から、式(1)に基づく抵抗力は、\(144~\rm{(N)}\)と推定されます。これらを比較したものが以下の図です。
非定常流れの計算であるため、初期条件の影響が残るシミュレーション直後の時刻においては、やや高めの抵抗を示しますが、シミュレーションの経過と共にその影響は流出境界からシミュレーション領域外へ流出します。初期条件の影響が十分小さくなったと考えられる時刻1~2秒以降では、（B）平板モデル（Plate）のケースでは、式(1)から算出される抵抗力付近を推移するのに対し、比較的地面に近い位置に設けられた（A）広告看板モデル（Signboard）のケースでは、20～30%程度抵抗力が増加していることが分かります。
流れ方向に垂直に設置された平板に関する抵抗係数というと、疑うことなく\(C_D=1.2\)を使うことが多いですが、本シミュレーション結果で示されるように、この抵抗係数はあくまで平板が他の物理境界の影響を受けない場合であって、壁や地面などの物体が比較的近い位置に存在する場合は、抵抗力も大きくなる場合があります。最も、\(C_D=1.2\)を用いた推定であっても、工学上は安全率を考慮するため、実用上の問題は起きないと考えられますが、抵抗係数の信頼性、不確定性について知っておいて損はありません。
