最も簡単な流体シミュレーション・ソフトウェア
最小ドラッグコンペ
1.計算対象
本チュートリアルでは、以下で紹介する「荷物」に空力パーツを追加し、物体全体として最小の流体抵抗を実現するための形状最適化を目的とします。荷物自体の形状の変更はできません。どのような空力パーツが最も小さな流体抵抗を実現できるか、複数のチームで競い合ってもよいでしょう。
Flowsquare+における流体抵抗の計算及び時系列計測方法は、こちらをご覧ください。
ここで紹介するシミュレーション実行に必要な全ての入力ファイルは、以下からダウンロードできます。
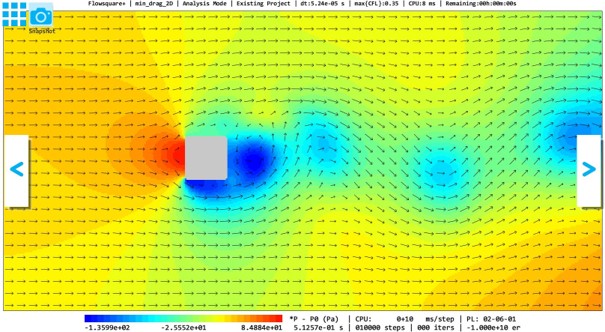
「荷物」ケース(空力パーツなし)
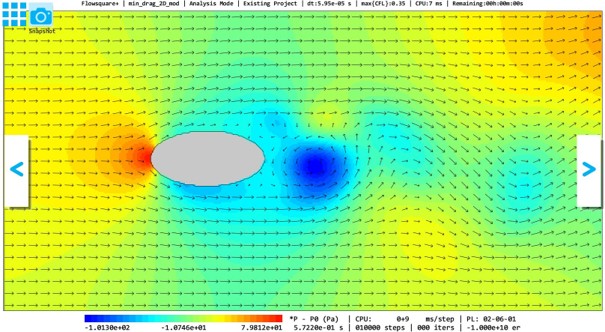
例1:楕円形状
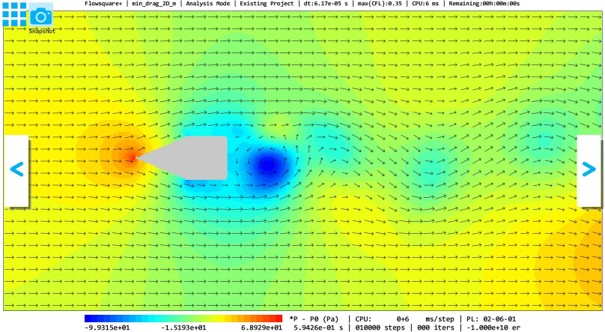
例2:荷物前方くさび
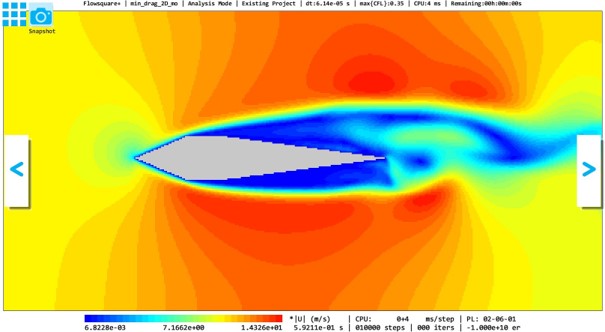
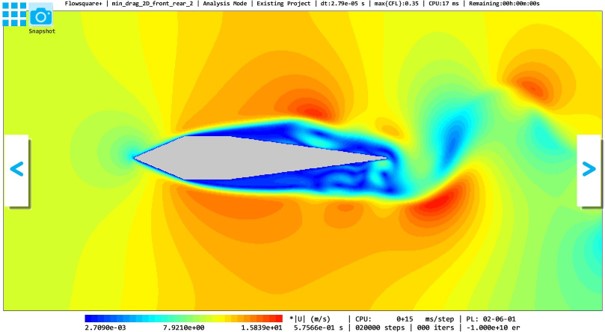
例3:荷物両端くさび
本シミュレーションは、一般的なIntel COREi7搭載のノートパソコン上で、parallel=3を用いて、1000ステップ20秒程度の計算速度です。
2.境界条件(空力パーツの追加)
本シミュレーションで用いる境界条件定義用ビットマップファイル(bcXY0.bmp)を以下に示します。流体は計算領域左から右へ向かって流入します。本シミュレーションでは、「荷物」ケースに指定されている紫四角形状物体に空力パーツを付加することで、流体抵抗の低減を実現します。追加する空力パーツの例として、以下の通り3つ紹介します。
3.計算パラメータの設定
本シミュレーションでは、空力パーツの追加のみで抵抗低減を実現します。複数チームなどで抵抗低減を競う場合には、数値パラメータは共通のものを使うのが良いでしょう。以下は、本シミュレーションにおいて特に大事なパラメータについての説明です。一般的な計算パラメータの説明は、こちらをご覧ください。
- cmode
0の流体解析モード(密度一定の液体、及び気体用)
- lx, ly
領域のX及びY方向サイズはそれぞれ1.0mと0.5m。
- nx、ny、nz
格子点数は、空間解像度を考慮して決定します。(nx, ny, nz) = (400, 200, 1)とし、各方向で同じ格子点間隔を用いています。
- rhoW
流体密度は、常温常圧の空気の値(1.2 kg/m^3)を使用。
- uinB
プリセット・カラーの青色で指定した流入流速は、10m/s (時速36km/h)。
4.シミュレーションの実行
上記リンクでダウンロードできる入力ファイルを変更する形で、荷物に自身の空力パーツを付加し、シミュレーションを開始します。シミュレーションまでの具体的な操作の流れは、こちらをご覧ください。また、流体抵抗の計算及び時系列計測方法は、こちらをご覧ください。
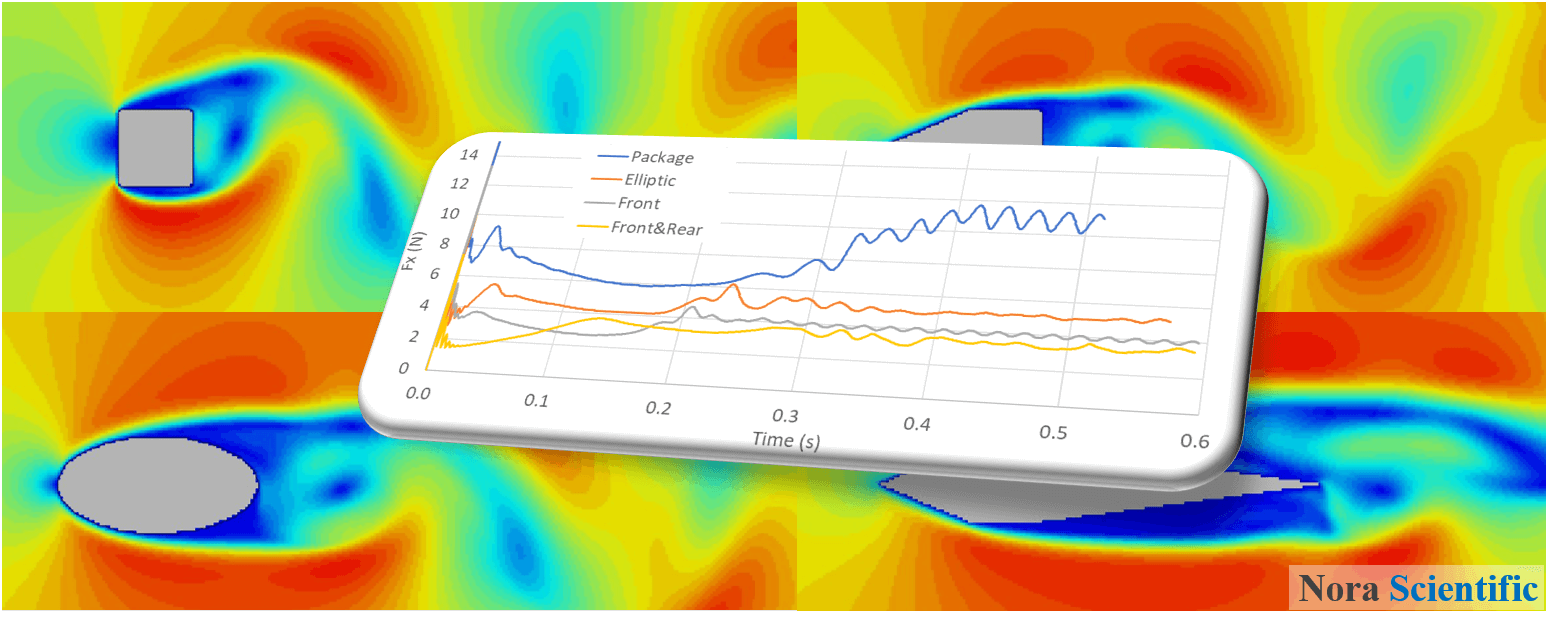
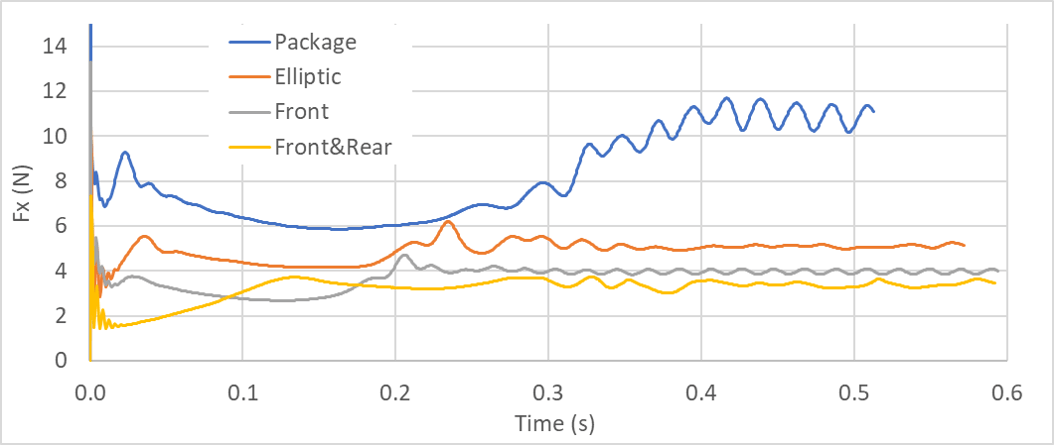
以下に、「荷物」をそのままシミュレーション領域に設置した場合の瞬時の流れ場と、荷物に楕円形状、前方くさび形状、両端くさび形状を付加した場合の瞬時の流れ場を示します。また、それぞれの場合における、物体に働く流れ方向の流体力の時間変化を示します。
今回の4ケースのうち、荷物の両端にくさび形状を付加したケースが最も小さい流体抵抗を実現しました。これ以下の流体抵抗を実現するにはどのような形状の空力パーツを付加すればよいでしょうか?
5.空間解像度の影響
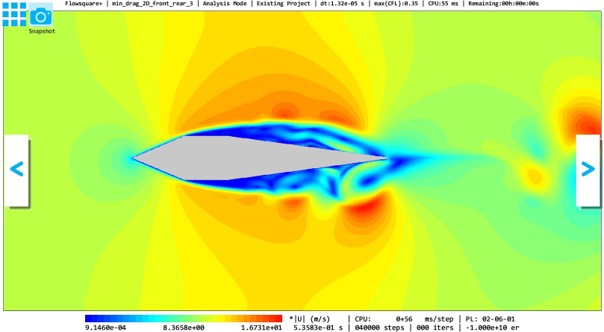
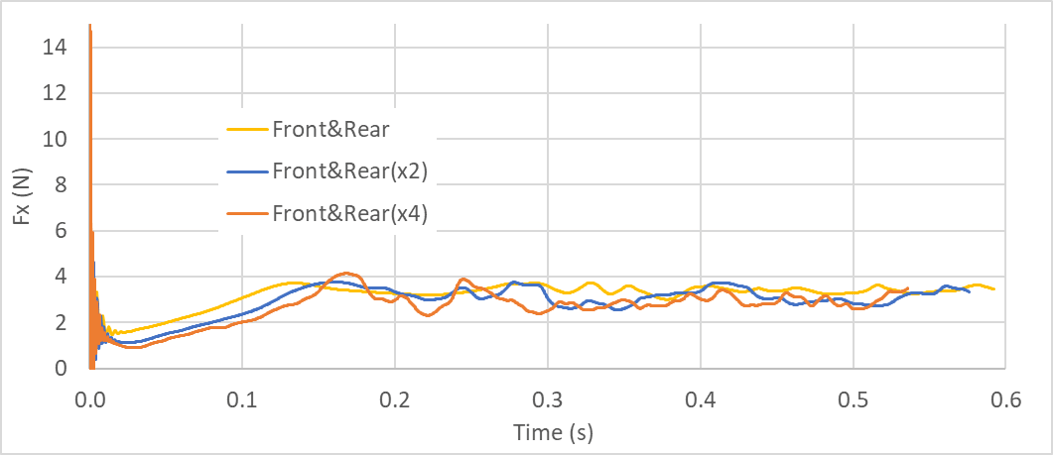
上記で計算される流体抵抗力の、シミュレーションの空間解像度への依存性を簡単に検証します。以下は、上記で紹介した空間解像度(規定値、nx=400, ny=200)、規定値の2倍(nx=800, ny=400)、規定値の4倍(nx=1600, ny=800)における両端くさびケースの流体速度の絶対値及び流体抵抗力の時間変化です。解像度に応じて時間刻み幅も小さくなるので、それぞれ、latts=10,000、latts=20,000、latts=40,000までシミュレーションを実施します。
比較すると、瞬時の流れ場は、空間解像度が大きくなると、より小さなスケールの速度変動が考慮される傾向にあり、また非定常運動の時間スケールも少し異なっていることが推測されますが、流体抵抗力に関して、定性的及び定量的に大きな傾向の変化は見られません。
 EN
EN