流体力学シミュレーション　オンライン・プログラミング口座

 

目次と講座サンプル（サンプル項目のみリンク表示）

※以下の★★★に従うだけで、本講座で解説する偏微分方程式を理解せずとも数値流体力学プログラムの作成が可能です。

  1. はじめに
    • 1.1　背景
    • 1.2　サンプルプログラムによる数値計算例
  2. 流体方程式計算の基礎
    • 2.1　流体問題への2大アプローチ
    • 2.2　空間分割化（離散化）と格子点の表記
    • 2.3　流れ場を支配する方程式群
    • 2.4　スカラーの輸送方程式
  3. インクの拡散過程のシミュレーション
    • 3.1　インクの拡散過程とそれを支配する方程式
    • 3.2　シミュレーションにおける1階微分
    • 3.3　シミュレーションにおける2階微分
    • 3.4　シミュレーションにおける時間積分（時間発展）
    • 3.5　拡散方程式：数値計算プログラミングに向けた式変形　★★★
    • 3.6　境界上の格子点の取り扱い（境界条件）
    • 3.7　インクの拡散過程シミュレーションのプログラミング（エクセル）
  4. インクの移流拡散過程のシミュレーション
    • 4.1　インクの移流拡散過程とそれを支配する方程式
    • 4.2　移流拡散方程式：数値計算プログラミングに向けた式変形　★★★
    • 4.3　境界上の格子点の取り扱い（境界条件）
    • 4.4　インクの移流拡散過程シミュレーションのプログラミング
  5. 2次元圧縮性流体シミュレーション
    • 5.1　2次元圧縮性流体支配方程式
    • 5.2　支配方程式の空間離散化
    • 5.3　オイラー法（1次陽解法）による時間積分
    • 5.4　境界の取り扱い（境界条件）
    • 5.5　補助方程式・初期条件
    • 5.6　空間フィルター（～人口粘性；簡易的）
    • 5.7　時間ステップ間隔の制限
    • 5.8　流れ場の境界条件（例）
    • 5.9　2次元圧縮性流体シミュレーション・プログラムの構成例　★★★
    • 5.10　2次元圧縮性流体シミュレーション・サンプルプログラム
  6. 2次元非圧縮性流体シミュレーション
    • 6.1　非圧縮性流体の特徴
    • 6.2　非圧縮性流体方程式の数値計算手法
    • 6.3　初期条件、計算条件の設定
    • 6.4　圧力項を無視した運動量方程式と近似速度
    • 6.5　境界条件
    • 6.6　圧力ポアソン方程式とその数値計算手法
    • 6.7　圧力効果による速度修正
    • 6.8　非圧縮性流体シミュレーションプログラムの構成例　★★★
    • 6.9　2次元費圧縮性流体シミュレーション・サンプルプログラム
  7. おわりに
    • 7.1　おわりに
  8. 【補足】シミュレーション結果（バイナリデータ）の可視化方法
    • A1. Viewsquareのダウンロードと使い方
    • A2. Paraviewの紹介
  9. お問い合わせ・相談

 

1．はじめに

1.1　背景

我々の身の回りには様々な流体現象が存在しています。天気や河川などのような自然現象のみならず、自動車や航空機など流体現象を応用した工業製品なども数多く存在し、これらの流れ場を数値解析により可視化する必要性は日増しに強くなっています。市場に出回る汎用ソフトを用いることで、ある程度流れ場の数値解析を行うことが可能ですが、用いるモデル、計算スキーム、境界条件など、ユーザーの要求全てを満たすには、利用者独自でユーザー定義関数などを通じて汎用ソフトに新たな機能を組み込む必要性が出てくるでしょう。

また、多くの流体解析ソフトは、ユーザーが指定するどのような入力パラメータに対しても、カラフルで滑らかな結果を出力するために、表には表れない”マジック”を使っており、この計算結果への効果は開発者でないユーザーが見積もることは困難です。流体解析シミュレーションコードを自ら製作することは、これらの問題点を理解するためにひと役買うでしょう。

本講座では、流体シミュレーションプログラムを製作する上で基礎となる計算手法をエクセル・Fortran／C言語計算プログラミングを含む実習を通じて習得します。数値計算プログラミングに特化した講座で、流体シミュレーションソフトウェアを自作したいが全く糸口が掴めない方、とりあえず数値計算の指針が欲しい方、一般的な流体シミュレーションソフトがどのようにして流れ場を解いているのか知りたい趣味人、学生、技術者などが主な対象です。

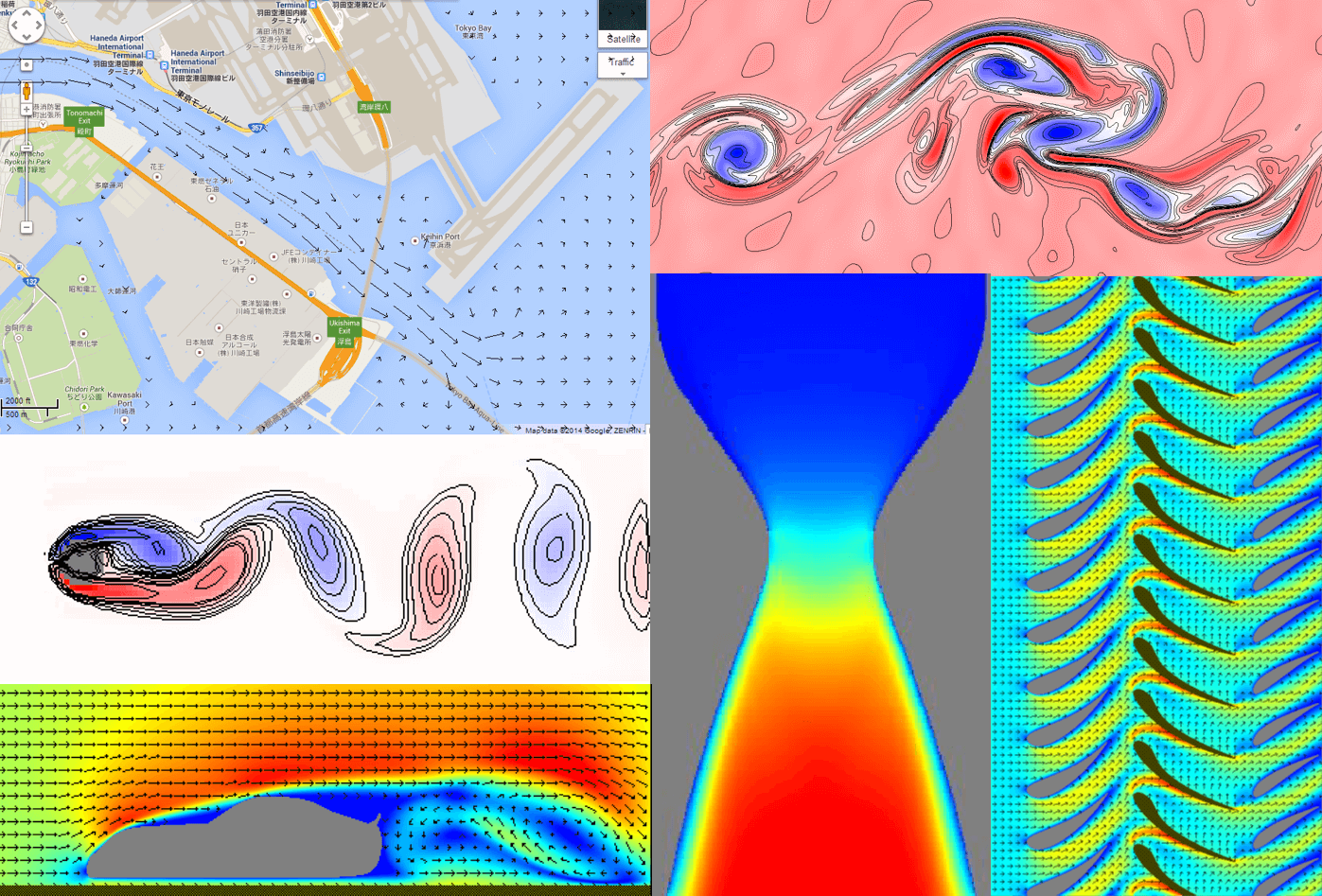
図1.1　Flowsquareを用いた流体シミュレーション結果の例。左上：多摩川の流速ベクトル、左中：カルマン渦列、左下：自動車周りの流れ、右上：混合層（ケルビン・ヘルムホルツ不安定性）、右下：ジェットエンジン・コンプレッサー、中下：超音速ノズル
図1.1　Flowsquareを用いた流体シミュレーション結果の例。左上：多摩川の流速ベクトル、左中：カルマン渦列、左下：自動車周りの流れ、右上：混合層（ケルビン・ヘルムホルツ不安定性）、右下：ジェットエンジン・コンプレッサー、中下：超音速ノズル

1.2　サンプルプログラムによる数値計算例

本講座では、始めにエクセルを活用した1次元拡散及び1次元移流拡散シミュレーションを通じて、流体数値シミュレーションの基礎を学び、その後、Fortran又はC言語による2次元流体シミュレーションプログラムの製作を目指します。具体的には、第5節では圧縮性流体のシミュレーションプログラム、そして第6節では非圧縮性流体のシミュレーションプログラムの基礎について学びます。両節においては、流体の基礎方程式（ナビエ・ストークス方程式）通りに記述されたサンプルコードを参考にすることで、数値流体力学や数値計算プログラミングの知識を深めることができます。

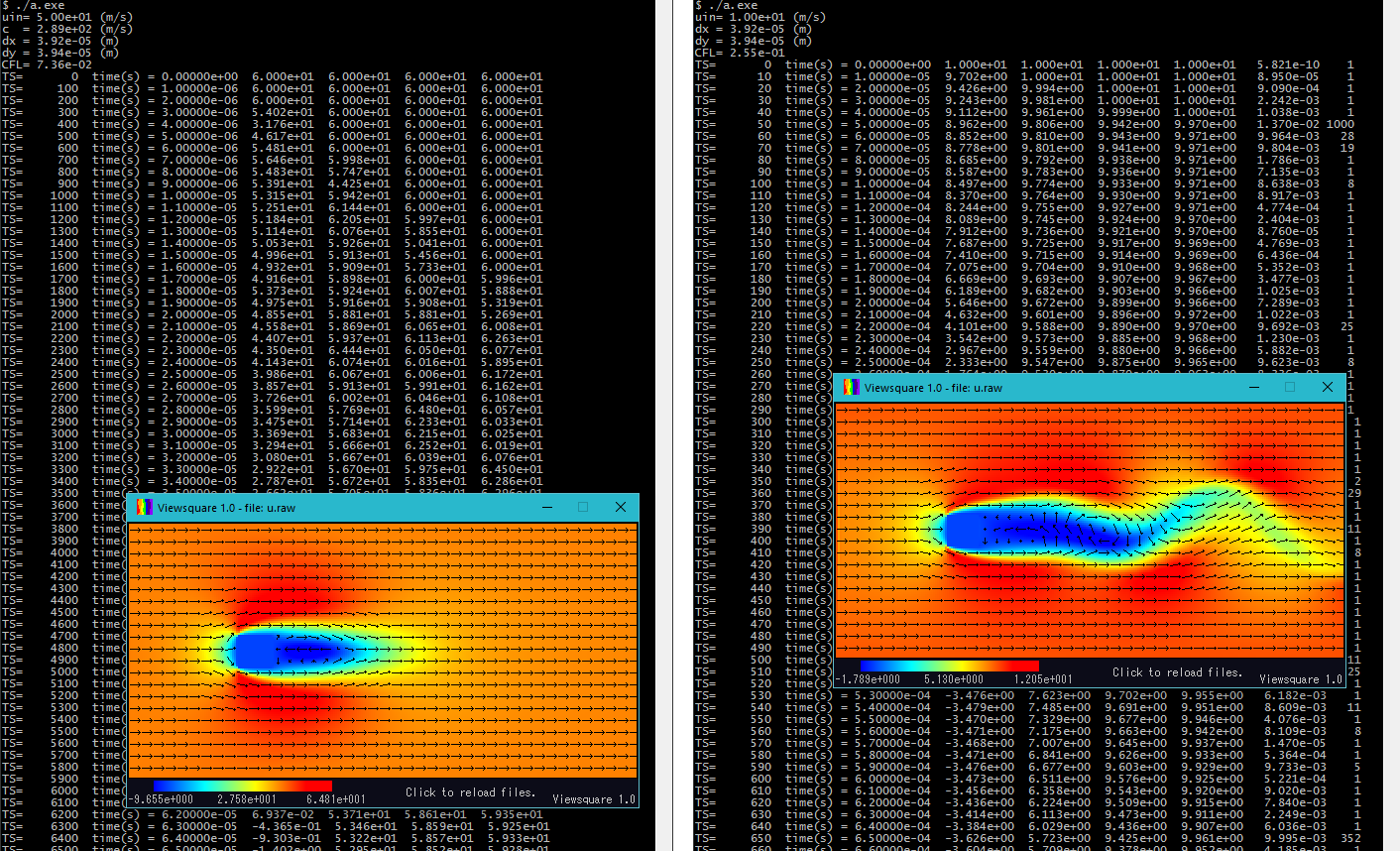
図1.2　サンプルコード実行による標準出力と流体数値計算途中結果の例（左：圧縮性流体計算、右：非圧縮性流体計算）
図1.2　サンプルコード実行による標準出力と流体数値計算途中結果の例（左：圧縮性流体計算、右：非圧縮性流体計算）

Top

 

2．流体方程式計算の基礎

2.1　流体問題への2大アプローチ

流体に限らず連続体と呼ばれる物体のとらえ方には二つの考え方があります。一つは、連続体を数多くの微小粒子の集まりととらえる方法、もう一つは連続体を連続体としてとらえる方法です。前者をラグランジュ的、後者をオイラー的な考え方と呼びます。

ラングランジュ的
連続体を微小粒子一つ一つの集まりと見る。それぞれの粒子は自然法則に支配されて動く。例えば、この方法では、連続体を高校物理で習うような放物線を描くボールの集まりと捉えると考えると分かり易い。ラグランジュ的な考えに基づくシミュレーションでは、計算領域に無数の粒子を配置し、それぞれの粒子の軌跡を計算する。以下の図のように、一人の観測者が無数のボール一つ一つの動きを追っている風に。
図2.1　ラグランジュ的方法
図2.1　ラグランジュ的方法
オイラー的
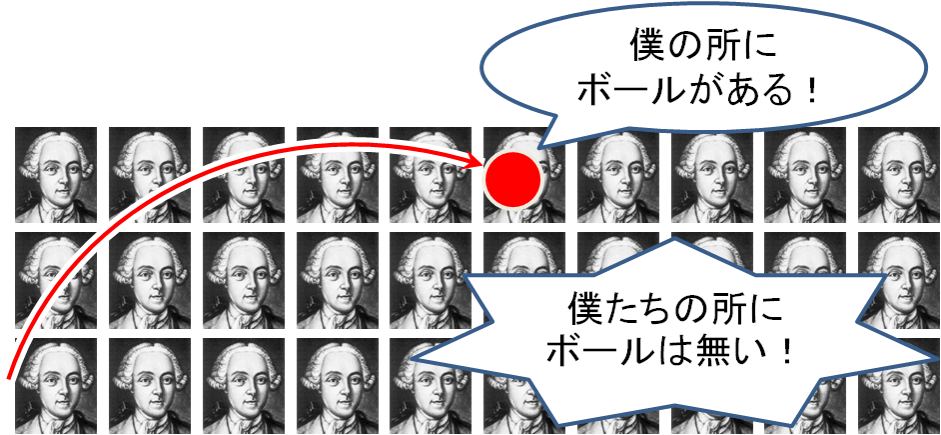
連続体をその名の通り、連続する“場”として見る。例えば、この方法では、対象領域の異なる位置（観測点）に非常に多くの観測者を配置し、それぞれの観測者は自分の分担領域のみの状況を報告する、というような考え方。例えば、以下の例では、各観測者がボールの有る無しを逐一報告することで、各人がボールの軌跡を最初から最後まで追わずともボールの位置が分かる。流体では、各観測者が自分の分担領域の状況（流速など）を報告することで、対象領域全体の流速分布が分かる。これは、連続体をばらばらの粒子の集まりと捉えるラグランジュ法と対象に、“場”の概念を用いている。
図2.2 オイラー的方法
図2.2 オイラー的方法

本講座では、連続体を場と捉えるオイラー的な概念を用います。現在販売されている多くの流体解析ソフトはオイラー的な概念に基づいた支配方程式を解いています。十分精度のよい数値計算手法を用いて支配方程式を解くと、ラグランジュ的・オイラー的にかかわらず同一のシミュレーション結果が得られます。

2.2　空間分割化（離散化）と格子点の表記

先に述べたように、オイラー的な考え方に基づいて流体場を考えるとき、対象となる（シミュレーション）領域に数多くの観測点を配置する必要があります。この観測点を流体シミュレーションでは格子点と言います。ではどのように格子点を配置すればよいでしょう？格子点の配置には数多くの手法がありますが、ここでは手軽で最も精度のよいデカルト座標系に基づいた格子を用いましょう。

皆さんの2次元流体シミュレーション領域が\(x\)方向（横）長さ\(L_x\) (m)、\(y\)方向（縦）長さ\(L_y\) (m)の長方形であったとします。この領域に、\(x\)方向と\(y\)方向それぞれ等間隔に、\(N_x\)個と\(N_y\)個の格子点を配置すると下の図のような格子点配置となります。

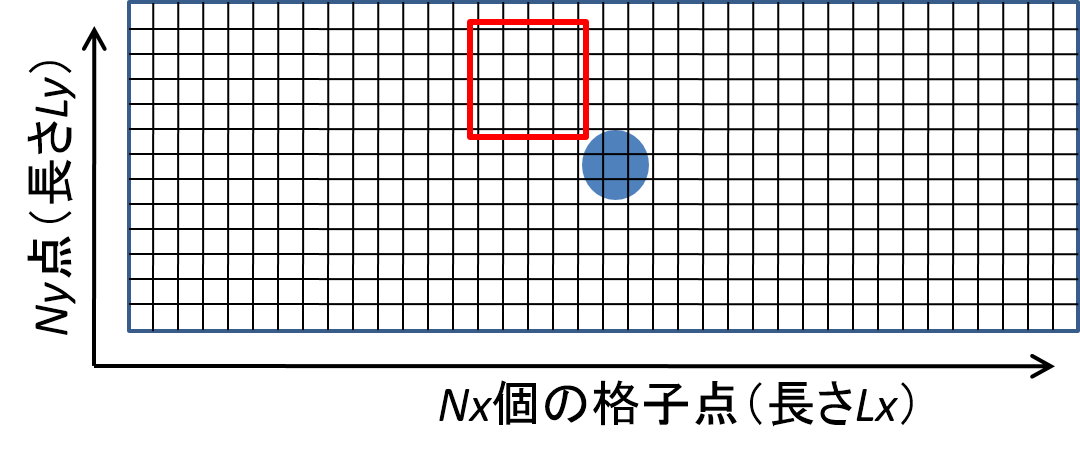
図2.3　2次元領域上に配置したデカルト格子
図2.3　2次元領域上に配置したデカルト格子

ここで、領域中の総格子点数は\(N_x\)と\(N_y\)の積となります。シミュレーションの条件として\(N_x\)と\(N_y\)を大きくすればするほど、上述のオイラー的概念における観測者の数が増えることになり、より詳細な観測（シミュレーション）が可能となります。上の図の赤い部分を拡大したものが下の図になります。\(x\)方向と\(y\)方向の格子点どうしの間隔は、それぞれ\(\Delta x\)と\(\Delta y\)と表記します。一般的に左から\(i\)番目、下から\(j\)番目の格子点の位置を\((i, j)\)と書くことがあります。また、ある物理量\(Q\)（例：速度など）に対して、格子点\((i, j)\)で観測される値を\(Q_{i,j}\)と表記します。この表記方法は本講座において今後使っていくので、ここでしっかりと覚えてください。

図2.4　2次元領域上に配置したデカルト格子の拡大図
図2.4　2次元領域上に配置したデカルト格子の拡大図

それでは、格子点に関して説明を進めるために、上記の2次元領域を単純化した1次元の領域を考えましょう。上と同じ要領ですが、1次元では領域は\(x\)方向に\(L_x\)の長さを持ち、その領域は\(N_x\)点の格子点で分割されています。格子点を用いて領域を分割することを専門用語では離散化と呼びます。下の図に、この1次元領域の\(i\)点周りを拡大した部分の模式図を示します。ある格子点\(i\)のすぐ左の点を\(i-1\)、すぐ右の点を\(i+1\)と表記します。この表記は後々頻出するので、慣れておいてください。例えば、\(i\)点から2点離れた点は、\(i-2\)と\(i+2\)、3点離れた点は、\(i-3\)と\(i+3\)と表記します。

図2.5　1次元領域上に配置した格子
図2.5　1次元領域上に配置した格子

具体例を考えましょう。下の図では、\(L_x\)の長さを持つ1次元領域を9点用いて分割することを考えます。従って、下の例では総格子点数\(N_x\)は9点です。両端の点を入れて9点なので、\(L_x\)の長さは8つの\(\Delta x\)と同じ長さになることはお分かりになるでしょうか？（実際に数えてみてください）

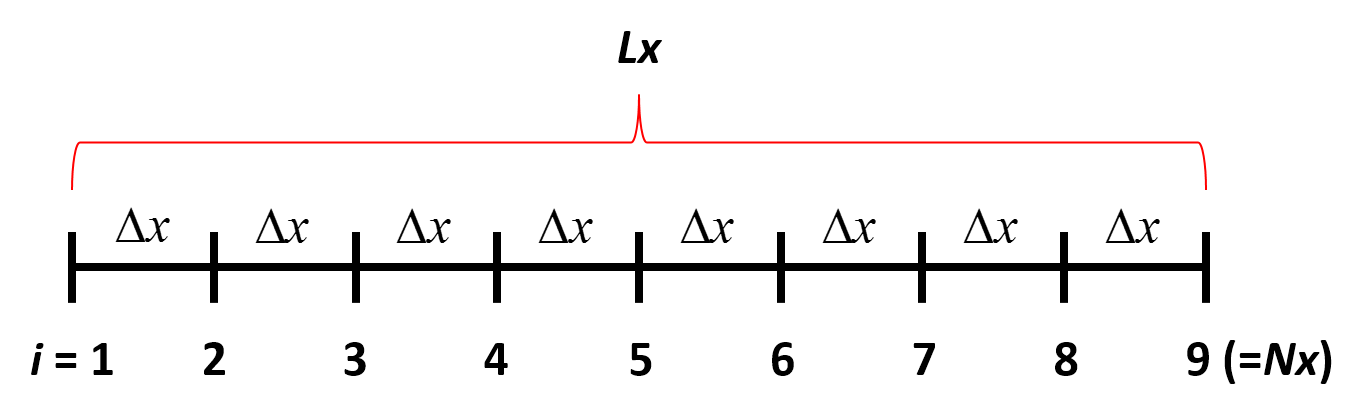
図2.6　1次元領域上に配置したデカルト格子と格子間隔の模式図
図2.6　1次元領域上に配置したデカルト格子と格子間隔の模式図

これを一般的に考えると、領域\(L_x\)の中には、\(N_x-1\)個の\(\Delta x\)が存在することになり、従って、\(\Delta x\)は\(L_x\)を\(N_x-1\)で割ったものと等価となります。この関係式は下の左式に対応します。また、任意の\(i\)番目の格子点の領域左端を距離0としたときの左端からの距離\(x\)は下の右式で表すことができます。この2つの式に、上図の値（\(N_x=9\)と\(i=1, 2, 3, \cdots, 9\)）を代入してみて実際に成り立つか確かめてみてください。

\begin{equation} \Delta x=\frac{L_x}{N_x-1}, x=(i-1)\cdot \Delta x. \end{equation}
式2.1　格子点間隔と領域長さ、格子点数の関係式

このように配置した格子点の各点上で、これから紹介する流体を支配する方程式群を解き、各格子点上での物性値（流体速度、圧力、流体密度）などの時間変化を求めます。

Top

 

7.　おわりに

7.1　おわりに

本講座で紹介した数値手法は、いずれも有限差分法に基づきます。他の流体数値解析の方法として、他にも有限体積法や有限要素法、スペクトル法、粒子法などがあります。また、同じ有限差分法を用いる数値手法にも、様々な精度の離散化手法、積分手法が存在し、数値アプローチも数多く提案されています。それぞれの数値手法には一長一短あり、最も優れた手法を一般的に決定することはできません。また、実在流体のシミュレーションには、乱流の寄与を考慮するために、非常に多くの計算資源を費やすか、乱流モデルを用いる必要があります。このように、本講座で紹介した項目は、数値流体力学を構築する知識のごく一部です。興味のある方は、さらに調べ進めることをお勧めします。

Top

 

【補足】シミュレーション結果（バイナリデータ）の可視化方法

A1. Viewsquareのダウンロードと使い方

Viewsquareは、本講座のために開発された無料で使える2次元バイナリデータ可視化ソフトです。講座で用いる格子点数\(N_x \times N_y\)格子点を有する出力データを読み込み、速度ベクトル表示及び物理量のカラー分布表示を行います。一般的なWindowsがインストールされたマシンで動作しますが、全てのマシン上での動作確認は致しておりません。ご了承ください。

ダウンロードしたViewsquareフォルダ内には、実行ファイル (Viewsquare.exe)と入力ファイル (grid.txt)が入っています。この実行ファイルと同じ階層に、本講座にて実施するシミュレーションの中間生成ファイル（サンプルコードでは、u.datやu.rawなど）を出力します。入力ファイルには、いくつか項目があり、これらを適切な値に設定した後、Viewsquare.exeを起動すると出力結果が表示されます。中間生成ファイルが刻々と上書きされるケースでは、起動したViewsquareの画面を右クリックすると、新しいファイルがリロードされます。

本講座では、サンプルコードをコンパイルすることにより生成される実行ファイルとViewsquare.exe、grid.txtを同一フォルダ内に置くことを推奨しています。同名で次々に上書きされるシミュレーション中間結果を右クリックのみで簡単に表示できます。

grid.txtに入力する項目として、q, u, v, nx, ny, skipbyte, flipがあります。qはカラー表示する物理量の中間生成ファイル名、u及びvは、速度\(u\)と\(v\)が格納されている中間生成ファイルのファイル名、nx及びnyは計算領域の\(x\)方向及び\(y\)方向格子点数、skipbyteは、中間生成ファイルのヘッダーのバイト数、flipは、\(x\)方向及び\(y\)方向を反転するか否かのフラグとなっています。以下は、本講座で公開しているFortranサンプルプログラムとC言語サンプルプログラムに適した入力内容です。どちらのケースもカラー表示する物理量は\(u\)となっています。

Fortranサンプルプログラムで生成される中間生成ファイル表示用入力ファイル


q        u.dat   // filename
u        u.dat   // filename
v        v.dat   // filename
nx        256   // nx
ny        128   // ny
skipbyte    4   // 0 (C), 4 or 8 (Fortran)
flip        2   // Flip (0:off, 1:x-x, 2:y-y, 3:x-y)

C言語サンプルプログラムで生成される中間生成ファイル表示用入力ファイル


q        u.raw   // filename
u        u.raw   // filename
v        v.raw   // filename
nx         256   // nx
ny         128   // ny
skipbyte     0   // 0 (C), 4 or 8 (Fortran)
flip         3   // Flip (0:off, 1:x-x, 2:y-y, 3:x-y)

A2. Paraviewの紹介

Paraviewは、オープン（無料）の多次元バイナリデータ可視化ソフトです。このツールを用いて可視化する場合、Fortranコードの以下の部分、


OPEN(10,FILE='xx.dat',FORM='UNFORMATTED')

を


OPEN(10,FILE='xx.raw',FORM='UNFORMATTED', ACCESS='STREAM')

と変更してください。変更点はファイル拡張子とACCESSオプションです。C言語コードでは変更の必要はありません。

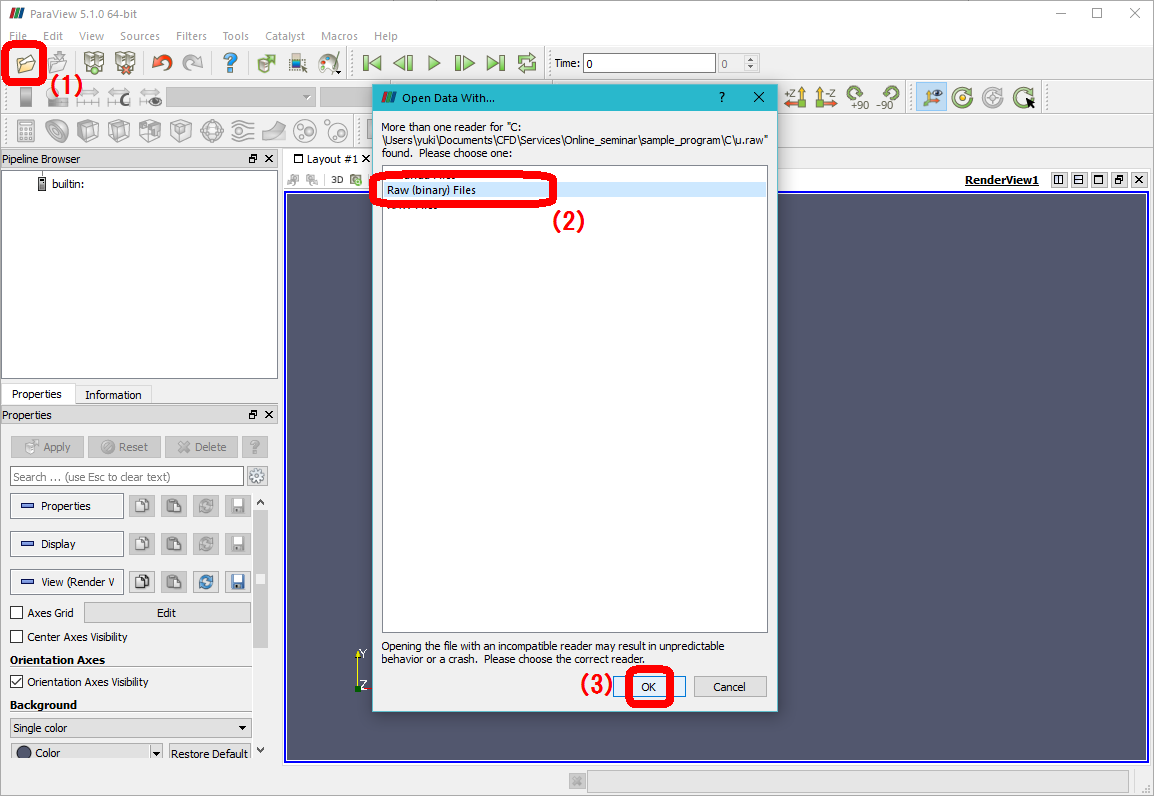
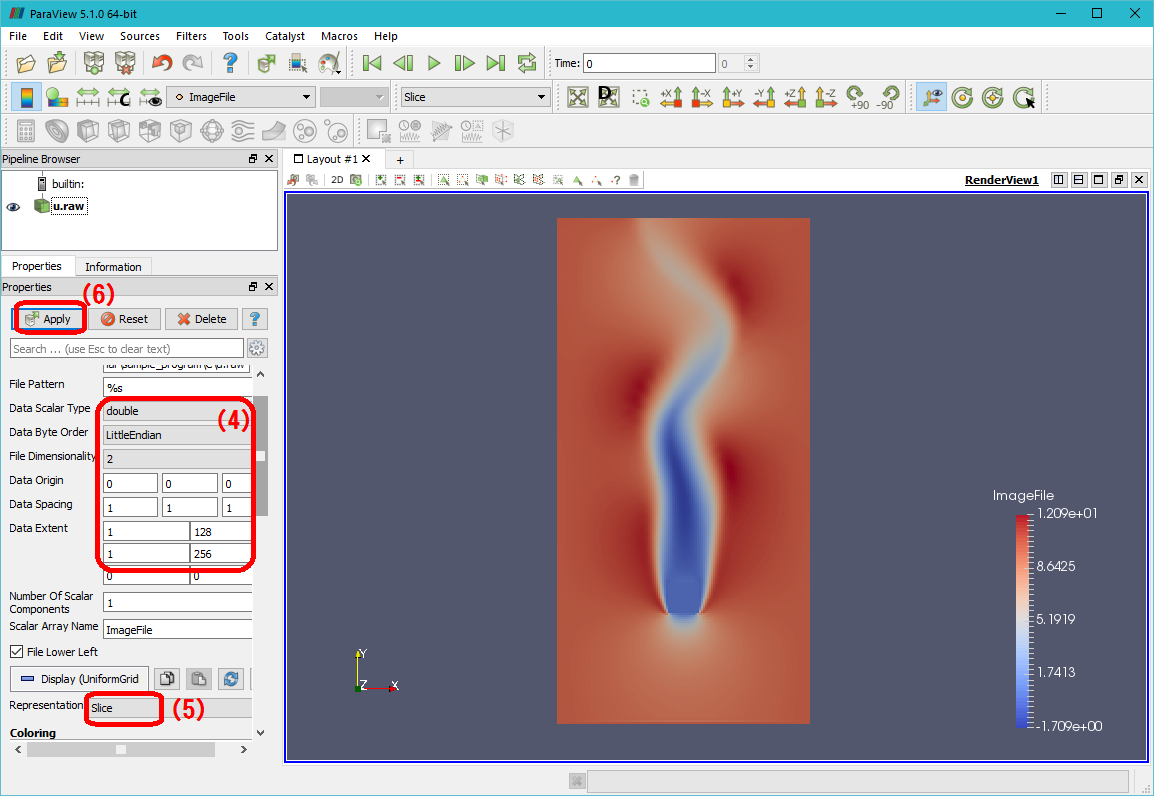
出力した中間生成ファイルの可視化方法は、まず、(1) ファイルオープンのアイコンをクリックし、(2) Raw (binary) ファイルを選択し、(3) OKボタンをクリックします。そして、下図を参考に、(4) データのファイルサイズなどを適切に指定し、(5) 表示方法のSliceを選択した後、(6) Applyボタンを押すと、選択した中間生成ファイルがカラー表示されます。

Paraviewの使い方(1)―(3)
Paraviewの使い方(1)―(3)
Paraviewの使い方(4)―(6)
Paraviewの使い方(4)―(6)

Top